Generative AI 4: Variational Autoencoders (VAEs)

Variational Autoencoders (VAEs) are a type of generative model that learns a probability distribution over the latent space of the data and can generate new, realistic data from that distribution. VAEs are used in applications like image generation, data compression, and anomaly detection.

4.1 VAE Architecture

The architecture of a VAE consists of two main components:

1. Encoder: Encodes the input data into a latent space.
2. Decoder: Decodes the latent representation back into the original data space.

The encoder maps the input \(\mathbf{x}\) into a latent variable \(\mathbf{z}\) (a lower-dimensional space). The decoder then reconstructs the input \(\hat{\mathbf{x}}\) from \(\mathbf{z}\).

However, unlike traditional autoencoders, VAEs encode the input as a probability distribution (mean and variance) rather than a deterministic point.

4.2 VAE Mathematical Model

Latent Variable Model:

Given an input \(\mathbf{x}\), the VAE assumes that it was generated by some latent variable \(\mathbf{z}\). The goal is to approximate the posterior distribution \(P(\mathbf{z}|\mathbf{x})\), but since this is intractable, VAEs use variational inference to approximate it with a simpler distribution \(q(\mathbf{z}|\mathbf{x})\), usually a Gaussian distribution.

Encoder (Inference Model):

The encoder outputs the parameters of the Gaussian distribution: Mean \(\mu\) and standard deviation \(\sigma\) of the latent variable distribution.

The encoded latent variable \(\mathbf{z}\) is then sampled from this distribution:

\[\mathbf{z} \sim q(\mathbf{z}|\mathbf{x}) = \mathcal{N}(\mathbf{z}; \mu(\mathbf{x}), \sigma^2(\mathbf{x}))\]

Decoder (Generative Model):

The decoder tries to reconstruct the original input \(\mathbf{x}\) from the sampled latent variable \(\mathbf{z}\). It outputs the probability of the reconstruction:

\[p(\mathbf{x}|\mathbf{z}) \sim \text{Decoder}(\mathbf{z})\]

VAE Loss Function:

The loss function of a VAE is composed of two terms:

1. Reconstruction Loss: Measures how well the decoder can reconstruct the input.

   \[\text{Reconstruction Loss} = \mathbb{E}_{q(\mathbf{z}|\mathbf{x})} [ \log p(\mathbf{x}|\mathbf{z}) ]\]

2. KL Divergence (Regularization Term): Encourages the latent variable distribution \(q(\mathbf{z}\\|\mathbf{x})\) to be close to the prior distribution \(p(\mathbf{z})\), typically a standard normal distribution \(\mathcal{N}(0, I)\).

   \[\text{KL Divergence} = D_{KL}(q(\mathbf{z}|\mathbf{x}) || p(\mathbf{z}))\]

The total loss function is:

\[\mathcal{L} = \text{Reconstruction Loss} + \beta \cdot \text{KL Divergence}\]

The KL Divergence regularizes the latent space to follow a normal distribution, while the reconstruction loss ensures that the model can accurately recreate the original data.

Implementing a VAE with PyTorch

Now, let’s implement a VAE using PyTorch to generate new data from the learned latent space.

Python Code:

import torch
import torch.nn as nn
import torch.optim as optim
from torchvision import datasets, transforms, utils
from torch.utils.data import DataLoader

# Define the VAE model
class VAE(nn.Module):
    def __init__(self):
        super(VAE, self).__init__()
        # Encoder layers
        self.fc1 = nn.Linear(28*28, 400)
        self.fc21 = nn.Linear(400, 20)  # Mean of latent variable
        self.fc22 = nn.Linear(400, 20)  # Log variance of latent variable
        
        # Decoder layers
        self.fc3 = nn.Linear(20, 400)
        self.fc4 = nn.Linear(400, 28*28)
    
    def encode(self, x):
        h1 = torch.relu(self.fc1(x))
        return self.fc21(h1), self.fc22(h1)  # Mean and log variance
    
    def reparameterize(self, mu, logvar):
        std = torch.exp(0.5 * logvar)  # Convert log variance to standard deviation
        eps = torch.randn_like(std)  # Random noise for reparameterization trick
        return mu + eps * std
    
    def decode(self, z):
        h3 = torch.relu(self.fc3(z))
        return torch.sigmoid(self.fc4(h3))
    
    def forward(self, x):
        mu, logvar = self.encode(x.view(-1, 28*28))
        z = self.reparameterize(mu, logvar)
        return self.decode(z), mu, logvar

# Loss function for VAE
def loss_function(recon_x, x, mu, logvar):
    BCE = nn.functional.binary_cross_entropy(recon_x, x.view(-1, 28*28), reduction='sum')
    KLD = -0.5 * torch.sum(1 + logvar - mu.pow(2) - logvar.exp())
    return BCE + KLD

# Load the MNIST dataset
transform = transforms.ToTensor()
train_dataset = datasets.MNIST(root='./data', train=True, download=True, transform=transform)
train_loader = DataLoader(dataset=train_dataset, batch_size=128, shuffle=True)

# Initialize model, optimizer, and train the VAE
model = VAE()
optimizer = optim.Adam(model.parameters(), lr=1e-3)

# Training the VAE
epochs = 10
for epoch in range(epochs):
    model.train()
    train_loss = 0
    for batch_idx, (data, _) in enumerate(train_loader):
        optimizer.zero_grad()
        recon_batch, mu, logvar = model(data)
        loss = loss_function(recon_batch, data, mu, logvar)
        loss.backward()
        train_loss += loss.item()
        optimizer.step()
    
    print(f'Epoch {epoch+1}, Loss: {train_loss/len(train_loader.dataset):.4f}')

# Generate new samples from the latent space
model.eval()
with torch.no_grad():
    z = torch.randn(64, 20)  # Sample from the standard normal distribution
    samples = model.decode(z).view(-1, 1, 28, 28)

# Visualize the generated samples
import matplotlib.pyplot as plt
grid_img = utils.make_grid(samples, nrow=8)
plt.imshow(grid_img.permute(1, 2, 0))
plt.show()

Output:

• Training Output: During training, the VAE’s loss (a combination of reconstruction loss and KL divergence) will decrease over epochs.

  Epoch 1, Loss: 189.7234
  Epoch 2, Loss: 142.6732
  ...
  Epoch 10, Loss: 103.2348
  

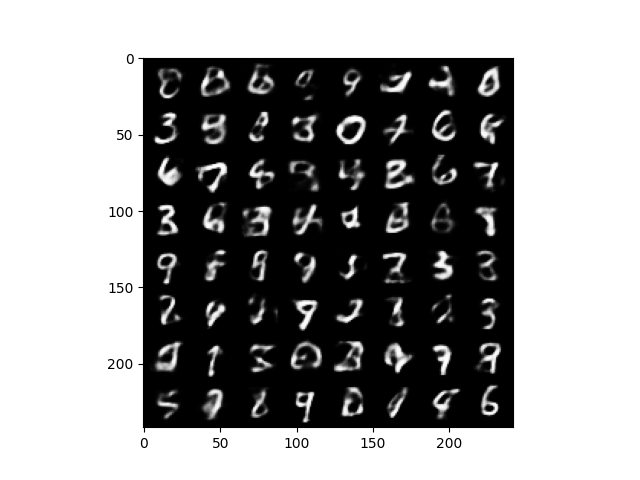
• Generated Samples: After training, the VAE can generate new images by sampling from the latent space. The images will look like handwritten digits (similar to the MNIST dataset).

Summary:

• VAEs are generative models that learn a probabilistic representation of the input data in a low-dimensional latent space.
• The encoder maps the input to a distribution over the latent space, and the decoder reconstructs the data from the latent space.
• The loss function of a VAE is a combination of reconstruction loss and KL divergence, which regularizes the latent space.
• VAEs can generate new data by sampling from the learned latent distribution.